《预防医学》 > 第二十一章　秩和检验

第一节　配对资料的比较

 

一、符号检验（sign test）

此法主要用于配对资料的比较，现以表21-1资料为例介绍其方法步骤。

例21.112名宇航员行前及返航后24小时的心率变化如表21-1所示，试问航行对心率有无影响？

表21-1宇航员航行前后的心率（次/分）及符号检验计算表

宇航员编号（1）	航前（2）	航后（3）	（2）-（3）差数的符号（4）
1	76	93	-
2	71	68	+
3	70	65	+
4	61	65	-
5	80	93	-
6	59	78	-
7	74	83	-
8	62	79	-
9	79	98	-
10	72	78	-
11	84	90	-
12	63	60	+

（一）建立检验假设

H₀：宇航对心率无影响，即差值的“正”、“负”号个数相等

H₁：宇航对心率有影响，即差值的“正”、“负”号个数不等

α=0.05

（二）将各对数据中，航前大于航后者记为“+”，航前小于航后者记为“-”，航前等于航后者记为“0”，列于表21-1第（4）栏。

（三）分别数出“+”“-”号的个数，并以“+”号的个数作为a，“-”号的个数作为b ,代入式（21.1）

公式（21.1）

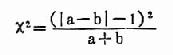
本例a=3,b=9

v=1，x²_0..05(1)=3.84,今x²=2.083＜3.84,P＞0.05,按α=0.05检验水准不拒绝H₀，因此尚不能认为宇航对心率有影响。

 

二、符号秩和检验（Wilcoxon法）

符号等级检验（signedrank test）是上述方法的改进，是在观察“+”“-”号个数的基础上亦考虑差值的大小，通过对差值偏秩求和进行检验的，故效果较好。仍以例21，1介绍其方法步骤。

表21-1宇航员航行前后的心率（次/分）比较

宇航员号（1）	航前（2）	航后（3）	差值（4）=（2）-（3）	秩次
				+（5）	-（6）
1	76	93	-17		9
2	71	68	3	1
3	70	65	5	4
4	61	65	-4		3
5	80	93	-13		8
6	59	78	-19		11
7	74	83	-9		7
8	62	79	-17		10
9	79	98	-19		12
10	72	78	-6		5
11	84	90	-6		6
12	63	60	3	2
合计				7	71

(一)建立假设

H₀：宇航对心率无影响，即差值的总体中位数M=0

H₁：宇航对心率有影响，即差值的总体中位数M≠0

α=0.05

（二）求各对数值的差数如表21-2第（4）栏

（三）编秩按差值的绝对值由小到大编秩，将秩次按差值的正负分两栏，如表21-2第（5）、（6）栏。注意：编秩时，遇有几个绝对值相等、符号相反的差值时，各取平均秩次；符号相同的相等差数，可不必取平均秩次；遇有差值为0的，则弃去不计，随之从相应的对子数n中减去。

（四）确定统计量t 分别求正负秩次之和，以绝对值较小者为统计量T，如表21-2第（5）、（6）两栏的合计。本例T=7。

（五）确定P值，作出推论

1．查表法用于对子数n≤25时，根据对子数n查附表21-1符号秩和检验临界值表。若现有统计量T值大于表中相应的界值T_0.05，则P＞0.05；若现有统计量小于或等于表中相应的T_0.05,则P≤0.05。本例对子数n=12，查表得T_0.01=7，本例T=7，故P=0.01，按α=0.05检验水准拒绝H₀，可认为宇航对心率有影响，使心率增快。由此看出符号秩和检验比符号检验效率高。

2．正态近似法对子数n＞25时，按式（21.2）计算统计u值。

公式(21.2)

因统计量为u值,按表19-3所示关系作出判断。